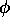 lj, are then transformed to two components,
lj, are then transformed to two components,
Clarkson University Relativistic Effective
Potential Database
L.A. Fefee, S.A. Wildman, G.A. DiLabio, T.M. Moffett, Jr., J.C. Peploski and P.A. Christiansen
Department of Chemistry
Clarkson University
Potsdam, New York 13699-5810
Background
The relativistic effective potentials in this data base were generated by the shape
consistent procedure proposed by Christiansen et al.1 and subsequently generalized to include
relativity2 using the methodology developed by Lee, Ermler and Pitzer3 . Briefly, one first solves
the Dirac-Hartree-Fock equations to obtain four-component atomic spinors. The four-component
valence spinors, 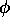 lj, are then transformed to two components,
lj, are then transformed to two components,
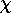 lj =
lj = 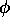 lj + Flj, (1)
lj + Flj, (1)
where Flj is itself a four-component spinor with large components that cancel the radial core-like
oscillations in the large components of the 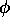 lj, but small components that completely cancel
those of the
lj, but small components that completely cancel
those of the 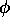 lj. The two-component pseudospinor,
lj. The two-component pseudospinor, 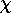 lj, is then effectively reinserted into the
DHF equation and the equation inverted to obtain the localized relativistic effective potential,
UREPlj. The total REP could then be written as an infinite expansion of the UljREP, each with the
appropriate projection operators. In practice, of course, the expansion is truncated at the lowest
angular momentum value, L, for which there are no longer any core-like oscillations in the large
component of
lj, is then effectively reinserted into the
DHF equation and the equation inverted to obtain the localized relativistic effective potential,
UREPlj. The total REP could then be written as an infinite expansion of the UljREP, each with the
appropriate projection operators. In practice, of course, the expansion is truncated at the lowest
angular momentum value, L, for which there are no longer any core-like oscillations in the large
component of 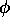 LJ. That is, the large components of FLJ disappear. Due to the minimal exchange
interaction between the core and higher l spinors and the absence of the Flj large components for
all l greater than L, this truncation is an excellent approximation. For use in conventional codes,
the REPs are then averaged and differenced for each l to form the corresponding averaged
relativistic effective potentials (AREP) along with spin-orbit operators.
LJ. That is, the large components of FLJ disappear. Due to the minimal exchange
interaction between the core and higher l spinors and the absence of the Flj large components for
all l greater than L, this truncation is an excellent approximation. For use in conventional codes,
the REPs are then averaged and differenced for each l to form the corresponding averaged
relativistic effective potentials (AREP) along with spin-orbit operators.
Averaged relativistic effective potentials with effective spin-orbit operators from Christiansen and coworkers2 are tabulated here as Gaussian expansions,
Ul(AREP or SO) = r-2 Clirnli exp(-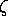 lir2), (2)
lir2), (2)
as originally proposed by Kahn4 and others. As such the AREP can be used without modification in standard software such as Gaussian-945 or the Columbus program package6. As required for the Columbus package, the tabulated spin-orbit operator coefficients have been multiplied by factors of 2/l.
While the molecular small components are not treated explicitly in the shape consistent
REP formalism, the small components, along with the core oscillations, are included in the
effective potential through the pseudospinor transformation and subsequent Fock equation
inversion. Indeed, implicit variation of the small components in subsequent molecular
environments is allowed by means of the projection operators.
| 1A | 2A | 3B | 4B | 5B | 6B | 7B | 8B | 8B | 8B | 1B | 2B | 3A | 4A | 5A | 6A | 7A | 8A | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | He | |||||||||||||||||
| Li | Be | B | C | N | O | F | Ne | |||||||||||
| Na | Mg | Al | Si | P | S | Cl | Ar | |||||||||||
| K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se | Br | Kr | |
| Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe | |
| Cs | Ba | La | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po | At | Rn | |
| Fr | Ra | Ac | ||||||||||||||||
| Ce | Pr | Nd | Pm | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu | |||||
| Th | Pa | U | Np | Pu | Am | Cm | Bk | Cf | Es | Fm | Md | No | Lr | |||||

Errors
In addition to errors resulting from the frozen core approximation, errors arise from the effective potential approximation as well. Fortunately in the shape consistent formalism the key sources are fairly easy to identify and minimize. For a single valence electron and ignoring relativity we can write the atomic Fock equation as,
(-1/2  2 -Znuc/r + Wcore)
2 -Znuc/r + Wcore)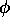 =
= 
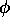 (3)
(3)
where Znuc is the nuclear charge, Wcore includes the coulomb and exchange interactions with the core, is the energy eigenvalue and is the valence eigenfunction. By partitioning along the lines of Eq. 1, the Fock equation becomes,
(1/2 2 +Znuc/r - Wcore +
2 +Znuc/r - Wcore +  )F + (-Zcore/r + Wcore)
)F + (-Zcore/r + Wcore)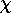 + (-1/2
+ (-1/2 2 -1/r)
2 -1/r)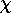 =
= 
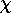 , (4)
, (4)
and the corresponding effective potential, UEP, is then,
UEP = {(1/2 2 +Znuc/r - Wcore +
2 +Znuc/r - Wcore +  )F + (-Zcore/r + Wcore)
)F + (-Zcore/r + Wcore)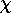 }/
}/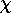 . (5)
. (5)
The last term on the right, {(-Zcore/r + Wcore)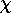 }/
}/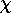 , is just the localized interaction potential
between the frozen core and the valence electron and, except for exchange in Wcore, is exact
within the frozen core approximation. The exchange terms fortunately include the core orbitals
as multiplicative factors and as a consequence their contributions in the valence space will decay
roughly according to the core/valence amplitude ratios. The other term, {(1/2
, is just the localized interaction potential
between the frozen core and the valence electron and, except for exchange in Wcore, is exact
within the frozen core approximation. The exchange terms fortunately include the core orbitals
as multiplicative factors and as a consequence their contributions in the valence space will decay
roughly according to the core/valence amplitude ratios. The other term, {(1/2 2 +Znuc/r -
Wcore +
2 +Znuc/r -
Wcore +  )F}/
)F}/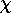 , however is entirely the result of the pseudoorbital transformation. This is the
strong repulsive term that prevents callapse into the core. This term will disappear in the valence
region where
, however is entirely the result of the pseudoorbital transformation. This is the
strong repulsive term that prevents callapse into the core. This term will disappear in the valence
region where 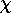 and
and 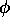 are identical, but in the inner valence (or outer core) region it may cause
serious problems. Clearly to ensure transferability one must choose the core space to be small
enough to minimize the local exchange approximation in the valence or bonding regions, and for
a given core space, one must form the pseudoorbitals such that the F go to zero as close to the
origin as possible.
are identical, but in the inner valence (or outer core) region it may cause
serious problems. Clearly to ensure transferability one must choose the core space to be small
enough to minimize the local exchange approximation in the valence or bonding regions, and for
a given core space, one must form the pseudoorbitals such that the F go to zero as close to the
origin as possible.
It has recently been shown that effective potential bond length errors observed for the
sixth-row main group elements were the result of F function tails in the generation of the 5f
pseudospinors. As a consequence the sixth-row main group REPs included in this data base are
from S.A. Wildman, et al.2f As seen in the table below, the new REPs give hydride bond lengths
in excellent agreement with experimental values.
Computed hydride bond lengths from new SPD type REPs used in selected intermediate
coupling CI (SICCI) calculations. Experimental values from ref. 7 are included for
comparison.
Method TlH PbH BiH
__________________________________________________________________________________________________________________
SICCI d-shell occupation
10(frozen d) 1.907 1.861 1.818
9 1.843 1.833 1.791
8 1.874 1.852 1.795
Experiment 1.870 1.839 1.805
__________________________________________________________________________________________________________________
Note the importance shown in the table of d-shell correlation (d8 occupation). From the above results it is absolutely essential that the 5d shell be included in the valence space for the sixth-row main group elements.
Errors will also arise from the Gaussian expansions of the AREPs and SO operators, but
these are generally fairly small. The AREPs and SO operators should not be truncated. Note however that the atomic orbital basis sets provided for use
with the REPs are of minimal size and should generally be supplemented with diffuse and
polarization functions where higher accuracy is required.
References
P.A. Christiansen, Y.S. Lee and K.S. Pitzer, J. Chem. Phys. 71, 4445 (1979).
(a) L.F. Pacios and P.A. Christiansen, J. Chem. Phys. 82, 2664 (1985); (b) M.M. Hurley,
L.F. Pacios, P.A. Christiansen, R.B. Ross and W.C. Ermler, J. Chem. Phys. 84, 6840
(1986); (c) L.A. LaJohn, P.A. Christiansen, R.B. Ross, T. Atashroo and W.C. Ermler, J.
Chem. Phys. 87, 2812 (1987); (d) R.B. Ross, J.M. Powers, T. Atashroo, W.C. Ermler,
L.A. LaJohn and P.A. Christiansen, J. Chem. Phys. 93, 6654 (1990); (e)R.B. Ross, J.M.
Powers, T. Atashroo, W.C. Ermler, L.A. LaJohn and P.A. Christiansen, Erratum, J.
Chem. Phys. 101, 1098 (1994); (f) S.A. Wildman, G.A. DiLabio and P.A. Christiansen, J.
Chem. Phys. (Submitted).
Y.S. Lee, W.C. Ermler and K.S. Pitzer, J. Chem. Phys. 67, 5861 (1977).
L.R. Kahn, P. Baybutt and D.G. Truhlar, J. Chem. Phys. 65, 3826 (1976).
M.J. Frisch, G.W. Trucks, M. Head-Gordon, P.M.W. Schlegel, M.A. Robb, E.S. Repogle,
R. Gomperts, J.L. Andres, K. Raghavachari, J.S. Binkley, C. Gonzales, R.L. Martin, D.J.
Fox, D.J. Defrees, J. Baker, J.J.P. Stewart and J. A. Pople, GAUSSIAN-94, Gaussian
Inc., Pittsburgh, PA (1992).
A.A.H. Chang and R.M. Pitzer, J. Am. Chem. Soc. 111, 2500 (1989), and references
therein.
K.P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV, Constants
of Diatomic Molecules, (Van Nostrand Reinhold, 1979).