Clarkson University
Guangming Yao
Division of Math and C.S.
Clarkson University
Office: SC 363
Office Phone: (315)268-6496
Current Research Interests:
1.
Radial Basis Function Neural Network and Machine Learning

2.
Stochastic Differential Equations and High-Dimension Partial Differential Equations

3.
High Performance Computing
4.
Radial Basis Function for Partial Differential
Equations.

INTRODUCTION:
The RBF-PDE
is the Radial Basis Function for the solution of PDE. This is a meshless
collocation method with global basis Functions. It is known to have exponentional convergence for interpolation problems. One
can descretize nonlinear elliptic PDEs by RBF method.
This results in modest size systems of nonlinear algebraic equations which can
be efficiently solved by standard software such as LINPACK, LAPACK etc.
Examples are published for 1D and 2D PDEs. These examples show high accuracy
with small number of unknowns, as compared with known results from the
literature.
OVERVIEW (by
Ed KANSA)
The
numerical solution of partial differential equations (PDEs) has been dominated
by either finite difference methods (FDM), finite element methods (FEM), and
finite volume methods (FVM). These methods can be derived from the assumptions
of the local interpolation schemes. These methods require a mesh to support the
localized approximations; the construction of a mesh in three or more
dimensions is a non-trivial problem. Typically with
these methods only the function is continuous across meshes, but not its
partial derivatives.
In
practice, only low order approximations are used because of the notorious
polynomial snaking problem. While higher order schemes are necessary for more
accurate approximations of the spatial derivatives, they are not sufficient without
monotonicity constraints. Because of the low order schemes typically employed,
the spatial truncation errors can only be controlled by using progressively
smaller meshes. The mesh spacing, h, must be sufficiently fine to capture the
functions partial derivative behavior and to avoid unnecessarily large amounts
of numerical artifacts contaminating the solution. Spectral methods while
offering very high order spatial schemes typically depend upon tensor product
grids in higher dimensions.... (Complete overview is here:PDF)
List of
people with E-mail addresses, Web-links is being appended. If you want your
name to be added to the list, please send E-mail to G. Yao at gyao@clarkson.edu.
Links - Web
resources
Boundary
element method Web page
5.
Applied Mathematics
1)
Excitation-Contraction Coupling Modeling
2)
Chemical Engineering Modeling
3)
Ground Water Modeling
1)
Excitation-Contraction Coupling Modeling


Fig. Left:
Multiple t-tubule geometry and its surrounding box domain. Right: 3D views of
the calcium concentrations at the calcium peak of 72 ms
when the subcellular model in placed 0 micrometer away from the cell membrane.
Spatial-temporal calcium dynamics due to calcium release, buffering, and
reuptaking plays a central role in studying
excitation-contraction (E-C) coupling in both normal and diseased cardiac
myocytes. We employ numerical algorithms to system of reaction-diffusion PDEs
to model such calcium behaviors.
2) Chemical
Engineering Modeling
Wood burning in wintertime poses a significant risk to human health. Apportioning
wood smoke during wintertime would be significantly useful. Levoglucosan
and methyl nitrocatechol have been considered as
primary and secondary markers respectively for apportioning wood smoke. We aim
to use PDE model and numerical simulations to find the lifetime of wood smoke
markers in wintertime conditions.
3)
Ground Water Modeling
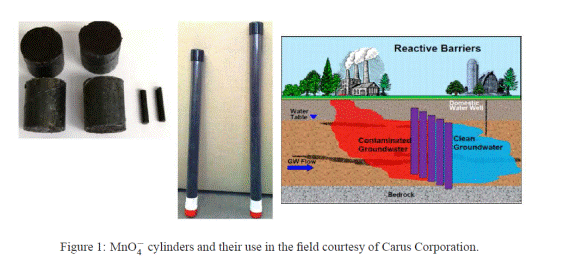
An emerging strategy for remediation
of contaminated groundwater is the use of permanganate cylinders for contaminant
oxidation. The cylinders, which are only a few inches in diameter, can be
placed in wells or pushed directly into the subsurface. This work focuses on
the modeling and simulation of the reactive process to better understand the
design of a group of cylinders for large scale contaminated sites. The
underlying model is a coupled system of nonlinear partial differential equations
accounting for advection, dispersion, and reactive transport for a contaminant
and the permanganate in two spatial dimensions. Radial Basis Functions
collocation method is used to simulate different spatial arrangements of the
cylinders to understand the behavior of the system and gain insight into
designing a remediation
strategy for a large-scale contaminated
region.
Let us try to test the performance of the cylinders produced by Carus Corporation. Please click here