A
GUIDE TO
POSITIVE
MATRIX FACTORIZATION
Philip
K. Hopke
Center
for Air Resources Engineering and Science
The
fundamental principle of source/receptor relationships is that mass
conservation can be assumed and a mass balance analysis can be used to identify
and apportion sources of airborne particulate matter in the atmosphere. This
methodology has generally been referred to within the air pollution research
community as receptor modeling [Hopke, 1985; 1991]. The approach to obtaining
a data set for receptor modeling is to determine a large number of chemical
constituents such as elemental concentrations in a number of samples.
Alternatively, automated electron microscopy can be used to characterize the
composition and shape of particles in a series of particle samples. In either
case, a mass balance equation can be written to account for all m chemical
species in the n samples as contributions from p independent sources
(1)
where xij is the ith
elemental concentration measured in the jth sample, fik is the gravimetric concentration (ng mg-1) of the ith element in
material from the kth source, and gkj
is the airborne mass concentration (mg m-3) of material from the kth source contributing to the jth
sample.
There
exist a set of natural physical constraints on the system that must be
considered in developing any model for identifying and apportioning the sources
of airborne particle mass [Henry, 1991]. The fundamental, natural physical
constraints that must be obeyed are:
1) The
original data must be reproduced by the model; the model must explain the
observations.
2) The
predicted source compositions must be non-negative; a source cannot have a
negative percentage of an element.
3) The
predicted source contributions to the aerosol must all be non-negative; a
source cannot emit negative mass.
4) The
sum of the predicted elemental mass contributions for each source must be less
than or equal to total measured mass for each element; the whole is greater
than or equal to the sum of its parts.
When developing
and applying these models, it is necessary to keep these constraints in mind in
order to be certain of obtaining physically realistic solutions.
The
critical question is then what information is available to solve equation (1).
It is assumed that the ambient concentrations of a series of chemical species
have been measured for a set of particulate matter samples so that the xij values are always known. If the sources that
contribute to those samples can be identified and their compositional patterns
measured, then only the contributions of the sources to each sample need to be
determined. These calculations are generally made using the effective variance
least squares approach incorporated into the EPA’s CMB model. However, for many
locations, the sources are either unknown or the compositions of the local
particulate emissions have not been measured. Thus, it is desirable to estimate
the number and compositions of the sources as well as their contributions to
the measured PM. The multivariate data analysis methods that are used to solve
this problem are generally referred to as factor analysis.
FACTOR
ANALYSIS
The
factor analysis problem can be visualized with the following example. Suppose a
series of samples are taken in the vicinity of a highway where motor vehicles
are using leaded gasoline and a steel mill making specialty steels. For these
samples, measurements of Pb, Br, and Cr are made.
This set of data can then be plotted in a three dimensional space as in Figure
1. A cloud of points can be observed.
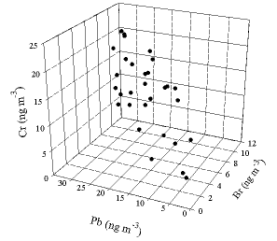
Figure 1. Three dimensional plot of simulated data.
However,
it is known that there are only two particle sources. The problem is then to
determine the true dimensionality of the data and the relationships among the
measured variables. That is goal of a factor analysis. In the case of this
example, the relationships can be observed with a simple rotation of the axes
so that we look down onto the figure so that the Cr axis sticks out of the
page. This view is seen in Figure 2. Now it can be seen that the data really cluster
around a line that represents the Pb-Br relationship
in the particles emitted by the motor vehicles. The Cr values are distributed
vertically and are independent of the other two elements. Factor analysis of
this problem would find two sources and provide the relationship between the
lead and bromine.
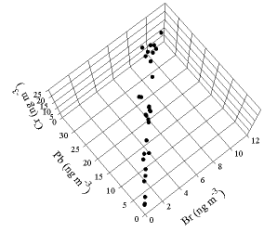
Figure 2. Plot of
the simulated data as viewed from above relative to the view in Figure 1.
.
Principal Component Analysis
The most common
form of factor analysis is Principal Components Analysis (PCA). This method is
generally available in most computer packages for statistical analysis. The PCA
results are generally calculated using an eigenvector analysis of a correlation
matrix [Hopke, 1985; Henry, 1991]. However, there are several problems
associated with such methods [Henry, 1987; Paatero
and Tapper, 1993, 1994]. The PCA model is based on a
series of n samples in which m chemical species have been measured. Thus,
equation (1) can be written in matrix form as
(2)
The X
matrix can also be defined in terms of the singular value decomposition.
(3)
where 
and 
are the first p
columns of the U and V matrices. The U and V
matrices are calculated from eigenvalue-eigenvector
analyses of the XX’ and X’X matrices, respectively. It can be shown
[Lawson and Hanson, 1974; Malinowski, 1991] that the second term on the right
side of equation (3) estimates X in the least-squares sense that it
gives the lowest possible value for
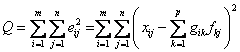(4)
The problem can
be solved, but it does not produce a unique solution. It is possible to
include a transformation into the equation.
where T is one of the potential infinity of transformation
matrices. This transformation is called a rotation and is generally included in
order to produce factors that appear to be closer to physically real source
profiles.
To
illustrate this problem, Figure 3 shows simulated data for ambient samples that
consist of mixtures of the soil and basalt source profiles [Currie et al.,
1984].
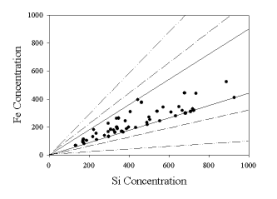
Figure 3. Simulated data showing
multiple possible source “profiles”
that could be used to fit the data.
This figure shows a plot of the iron and silicon
values for a series of simulated samples. There need to be two profiles to
reproduce each data point, but these “profiles” could range from the original
axes to any of the other pairs of lines. Because there are no zero valued
source contributions, the solid lines are not the “true” profiles. The true
source profiles lie somewhere between the inner solid lines that enclose all of
the points and the original axes, but without additional information, these
profiles cannot be fully determined. This is the problem that was presented by
Henry [1987] when he described factor analysis as “ill-posed.”
Paatero and Tapper [1993] have
shown that in effect in PCA, there is scaling of the data by column or by row
and that this scaling will lead to distortions in the analysis. They further
show that the optimum scaling of the data would be to scale each data point
individually so as to have more precise data having more influence on the
solution than points that have higher uncertainties. However, they show that
point-by-point scaling results in a scaled data matrix that cannot be
reproduced by a conventional factor analysis based on the singular value
decomposition. Thus, an alternative formulation of the factor analysis problem
is needed.
Positive
Matrix Factorization
Mathematical
Framework
This
new approach to factor analysis is Positive Matrix Factorization (PMF). In this
new method, the problem of non-optimal scaling has been explicitly addressed.
In order to properly scale the data, it is necessary to look explicitly at the
problem as a least-squares problem. To begin this analysis, the elements of the
"Residual Matrix," E are defined as
(6)
where i =1,..., m
elements
j
=1,..., n samples
k=1,..., p sources
An "object
function," Q, that is to be minimized as a function of G and F is given by
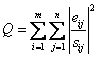(7)
where sij is an
estimate of the “uncertainty” in the ith variable
measured in the jth sample. One of the critical
aspects of using the PMF method is the choice of these uncertainties and this
process will be discussed in more detail below. The factor analysis problem is
then to minimize Q(E) with respect to G and F with the
constraint that each of the elements of G and F is to be non-negative.
Initially
the problem was solved iteratively using alternating least squares [Paatero and Tapper, 1993]. In alternating least-squares, one of the
matrices, G or F, is taken as known and the chi-squared is minimized with
respect to the other matrix as a weighted linear-least-squares problem. Then
the roles of G and F are reversed so that the matrix that has just been
calculated is fixed and the other is calculated by minimizing Q. The process
then continues until convergence. However, this process can be slow.
In
order to improve performance, each step in the iteration was modified so that
modifications are made to both matrices [Paatero and Tapper, 1994]. Subsequently, Paatero
[1997] describes a global optimization scheme in which the joint solution is
directly determined. This program, PMF2, is able to simultaneous vary the
elements of G and F in each iterative step. The model will be designated as PMF
while the program used to solve the model will be designated PMF2.
In
PMF2, the non-negativity constraint is imposed through the use of a penalty
function in an enhanced function, . Regularization can
also be imposed to reduce rotational freedom so that the enhanced object
function is defined as
Where P(G) and P(F) are
penalty functions that prevent the factors G and F from becoming negative. R(G) and R(F) are regularization functions that remove some
of the rotational indeterminacy. For the unconstrained case, α
and ß are set to zero. However, the regularization terms are always
present in the analysis. All of the coefficients, α, β, γ, and δ, are given
smaller values during the iterations so that their final values are negligible
but not zero. In practice, the log functions are approximated by a
Subsequently,
it was found useful to have a more versatile program for solving a more general
set of problems. Xie et al. [1999b] found that
a model that includes both terms like equation (1) and trilinear
terms (product of 3 factors) provided a better fit to the data. Paatero [1999] has developed a second program, the Multilinear Engine (ME), that can also solve the positive
matrix factorization problem but with an approach that provides more
flexibility in specifying the model. There are differences in the computational
approach between PMF2 and ME. At this time, PMF2 has been more widely used and
tested, but recent work with ME has shown the value of being able to build more
complex data analysis models.
Estimation of
Weights
The
solution to the PMF problem using either program depends on estimating
uncertainties for each of the data values used in the PMF analysis. There are
three types of values that are typically available. Most of the data points
have values that have been determined, xij,
and their associated uncertainties, σij.
One of the values of nuclear analytical methods is that it is easy to provide
an estimate of the uncertainty associated with the measurement of each element
in each sample. These uncertainties then serve as a starting point for the
weight estimation.
There
are samples in which the particular species cannot be observed because the
concentration is below the method detection limit. Finally there are samples
for which the values were not determined. These latter two types of data are
often termed “missing” data. However, there are qualitative differences between
them. In the below detection limit samples, the value is known to be small, but
the exact concentration is not known. In the case where values could not be
determined, the value is totally unknown.
Polissar et al. [1998] has suggested the following
for the concentration values and their associated error estimates:
For
determined values
For
below limit of detection values (9)
For
missing values
For
determined values
For below
limits of detection values (10)
For
missing values
Where 
, 
, and 
are the
measured concentration, the analytical uncertainty, and the method detection
limit, respectively, for sample i,
element j, and sampling site k, 
is arithmetic
mean of the detection limit value for the element j and the sampling
site k; and 
is the
geometric mean of the measured concentration of the element j at
sampling site k. Half of the
average detection limits were used for below detection limits values in the
calculations of the geometric means.
The
detection limits specified the error estimates for low concentration while
uncertainties provided the estimation of errors for high concentration of
element j. Error estimates for the determined values were usually less
than 50%; were used for below detection limits values and corresponding
relative error estimates from 100% to 250% were used for these values according
to equation (10). Geometric mean values with the corresponding error estimates
equal to 4 times these values were used for the missing values so that relative
error estimates for missing values were equal to 400%. Thus, both the values
that were used for the below detection limit values and the values that were
used for missing values had much lower weights in comparison to actually
measured values.
“Missing”
means that some elemental concentrations are missing for a specific sample but
the concentration of at least one element had been reported for the particular
sample. Then the missing concentrations and corresponding error estimates of
other elements were calculated according to equations (9) and (10).
Alternatively, heuristic error estimates, sij,
for a given xij can be estimated based on
the data point and its original error estimate, σij.
The general equation is
(11)
with
C1 =
σij
C2 =
0 except for Poissonian processes
C3 = dimensionless
values between 0.1 – 0.2 are typically chosen so that the relative uncertainty
of each data set was reasonable.
Similar
approaches were used for estimating weights in other recent applications [Yakovleva et al., 1999; Chueinta
et al., 2000].
PMF
also offers an option when it is not possible to fully specify the individual
data point errors. Models can be developed for this problem using a
distribution that is known a priori. For environmental data, a lognormal
model is available in which the user has to specify the logarithm of the
"geometrical standard deviation" (log(GSD))
for each measured value. It is often sufficient to use the same value for all
measured points if all of the values are truly lognormally
distributed. However, zero values cannot occur in a lognormal distribution and
yet such values can occur. These values make the factorization unreliable if
they are processed under the assumption of pure lognormality.
Then the assumption of lognormality needs to be
modified. PMF offers the option to assume that there is an additional normal
error superimposed onto the lognormal distribution. The method detection limit
can be used as this additional error. The statistical properties of this model
are not fully known. The expectation value of Q does not equal the degrees of
freedom in lognormal model. However, PMF provides an estimate of the expected
value of Q
Another
important aspect of weighting of data points is the handling of extreme values.
Environmental data typically shows a positively skewed distribution and often
with a heavy tail. Thus, there can be extreme values in the distribution as
well as true “outliers.” In either case, such high values would have
significant influence on the solution (commonly referred to as leverage). This
influence will generally distort the solution and thus, an approach to reduce
their influence can be a useful tool. Thus, PMF offers a “robust” mode. The
robust factorization based on the Huber influence function [Huber, 1981] is a
technique of iterative reweighing of the individual data values. The least
squares formulation, thus, becomes to
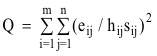
(12)
where
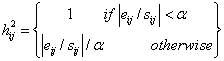
α = the outlier
distance and the value of α = 4.0 was chosen
It is generally
advisable to use the robust mode when analyzing environmental data.
Our
experience has generally found that the lognormal model and the robust mode
provide the best results for typical particulate composition data. For the NOAA
aerosol data from Barrow [Polissar et al.,
1999], it was found that the lognormal model produced reasonable results but
that the robust mode caused problems in terms of results that made physical
sense. However, these data consist of monthly mean particle counts and light
scattering efficiency and apparently behave somewhat differently from typical
particle composition data.
Algorithms
Over
the past several years several approaches to solving the PMF problem have been
developed. Initially, a program called PMF2 utilized a unique
algorithms [Paatero, 1997] for solving the
factor analytic task. For small and medium-sized problems, this algorithm was
found to be more efficient than ALS methods [Hopke et al., 1998]. It has
now been applied to a large number of problems [Anderson et al., 2001;2002;
Buzcu et al., 2003; Begum et al., 2004;
Chueinta et al., 2000; Claiborn
et al., 2002; Gao et al.2003; Hien et al., 2004; Huang et al., 1999; Kim
and Hopke, 2004a&b; Kim et al., 2003a&b; 2004a&b; Larsen and
Baker, 2003; Lee et al., 1999; 2002; 2003; Maykut
et al., 2003; Miller et al., 2002; Paterson et al., 1999; Polissar et al., 1996; 1998; 1999; 2001; Prendes et al., 1999; Qin and Oduyemi,
2003; Qin et al., 2002; Ramadan et al., 2000; Xie
et al., 1999b]. Huang et al. [1999] analyzed elemental
composition data for particulate matter samples collected at Narragansett, R.I.
using both PMF and conventional factor analysis. They were able to resolve more
components with more physically realistic compositions with PMF. Thus, the PMF
approach has some inherent advantages particularly through its ability to
individually weight each data point. PMF is somewhat more complex and harder to
use, but it provides improved resolution of sources and better quantification
of impacts of those sources than PCA [Huang et al., 1999].
Subsequently,
an alternative approach that provides a flexible modeling system has been
developed for solving the various PMF factor analytic least squares problems [Paatero, 1999]. This approach, called the multilinear engine (ME), has been applied to an environmental
problem [Xie et al., 1999a] and has only
recently been applied to a limited number of complex modeling problems [Chueinta et al., 2004; Hopke et al., 2003;
Kim et al., 2003c; Paatero and Hopke, 2002; Paatero et al., 2003].
Guidance on
the Use of PMF2
Initial Data
Evaluation
There
are severe limits to the extent that standard routines can be developed to
pre-process complex airborne particulate matter compositional data sets. In our
extensive experience in exploring a large number of data sets, there are unique
aspects to virtually every data set. Thus, there will need to be clear caveats
provided to the user of these procedures to indicate that data evaluation is
not something that can be fully accomplished with standard procedures.
Variables
can be categorized into several categories [Paatero
and Hopke, 2003]. A variable will be called “a weak variable” if it
contains signal and noise in comparable amounts. Similarly, variables
containing much more noise than signal are termed “bad variables”. It is
problematic to give precise definitions of the terms weak and bad variables. On
one hand, currently there is not much practical experience about the suggested
techniques. On the other hand, the shapes of distributions will be different
for different variables. This should be taken into account when defining what weak
or bad means. Also, the definition will depend on the representation of
smallest concentrations: are they given as measured, or are they censored so
that only the detection level (DL) is given instead of such actual values that
are “Below Detection Level” (BDL).
The
signal to noise ratio is calculated as defined in Paatero
and Hopke (2003).
(13)
A
variable is defined to be weak if its S/N is between 0.2 and 2. If S/N < 0.2, then a variable is defined to be bad. As already suggested, these limits
are somewhat arbitrary. The intention is that in a weak variable, there are
similar amounts of signal and noise, while there is clearly less signal than
noise in a bad variable.
For
censored data, a tentative definition is based on the number mDLj of BDL values in column j.
Denote the (average) detection limit for censored values in column j by δj. Then variable j is defined to be weak
if
(14)
An example of
this definition: assume that 50% of values xij
are BDL. Denote by Xj the average
of those values xij that are above δj. Then Equation (14) reduces to 0.2< Xj/δj <2. Based on the
initial work of Paatero and Hopke (2003), the
following recommendation is made.
In
PMF, an uncertainty is specified for each individual data value. If these
uncertainties are specified too small or too large in comparison to the true
error level of a certain variable, then an overweighting or downweighting
of the variable occurs. Regarding weak/bad variables, the main result of this
work is that even a small amount of overweighting is quite harmful and should
be avoided. In contrast, moderate downweighting, by a
factor of 2 or 3, never hurts much and sometimes is useful. Thus, it is
recommended to routinely downweight all weak
variables by a factor of 2 or 3. This practice will act as insurance and
protect against occasions when the error level of some variables has been
underestimated resulting in a risk of overweighting such variables. Regarding
bad variables (where hardly any signal is visible from the noise), the
recommendation is that such variables be entirely omitted from the model. If
this is not desirable, then such variables should be strongly downweighted, by a factor of 5 or 10.
The
procedure just described provides a overall view of a
variable. It is also necessary to examine individual data values. Typically one
examines the time series of the individual input variables looking for unusual
patterns or values in the data. Similarly, the complete set of variable biplots should be plotted and explored. These can been examined to identify unusual points and potential
relationships that should appear in the extracted factors.
Estimation of
the Number of Factors
One
of the most difficult issues in factor analysis is the determination of the
number of factors to use in the model. There is no unequivocal method to
identify the correct number of factors. There are a number of guidelines that
can be used included the extracted Q-value, the nature of the scaled residual
distributions, and the interpretability of the extracted factors.
The
theoretical Q-value should be approximately equal to the number of degree of
freedom, or approximately equal to the total number of data points in the data
array. If the errors are properly estimated, then it can be seen that fitting
each data point such that the reproduced value to within the estimated error value
will contribute a value of approximately 1 to the Q value. Thus, it is tempting
to examine the estimated Q value as a function of the number of factors to
determine the number of factors to retain. However, this approach can be
misleading if the data point uncertainties are not well determined. This
problem has been observed when only the measured uncertainties are used as the
weights. This problem can be minimized by using weights like are presented in
Equation 10 or using a model for the data point errors as described in Equation
11. It is useful to look at the changes in Q as additional factors are
calculated since after an appropriate number of factors are included in the
fit, additional factors will not result in significant further improvements in the
Q-value. Such behavior can be observed in Yakovleva et
al. [1999]. Thus, PMF suffers from the same difficulties in determining the
correct number of factors as all other forms of factor analysis.
As
one of the methods to determine the quality of the fit, the residuals, eij, are examined. Typically the distributions
of the residuals are plotted for each measured species. It is desirable to have
symmetric distributions and to have all of the residuals within + 2
standard deviations. If there is skewness or a larger
spread in the residuals, then the number of factors should be reexamined.
One
of the disadvantages of a least-squares approach is that it can yield multiple
solutions depending on the initial starting point. As part of the PMF program,
it is possible to initiate random values in the F and G matrices as the
starting point for an analysis. It is generally advisable to perform the
analysis several times (typically 5) to be certain that the same solution is
obtained. It has been our experience that one of the tests of the best
selection of the number of factors is that one does not obtain multiple
solutions or obtains at most one alternative solution. With greater or fewer
factors than optimum, multiple solutions are more often obtained.
Finally,
the quality of the solution must be examined in terms of how easily can the
factors be identified as source types and do the corresponding source
contribution patterns make sense. Source profiles can be compared to those that
exist in the literature or those that have been locally measured. In each data
set there are often specific events that can be identified. For example, in
areas where the weather can be divided into wet and dry seasons, there should
be appropriate differences in the source contributions during these two
periods. If there is known activities such as construction, wildfires, or major
transboundary episodes, these events should appear in
the time series record of contributions.
Factor
Rotations
In
general, this type of bilinear factor analysis will have rotational ambiguity.
There will not be a unique solution even though there will be a global minimum
in the least-squares fitting process. The addition of constraints can reduce
the rotational freedom in the system, but non-negativity alone does not
generally result in a unique solution. One of the key features of PMF is that
the rotations are part of the fitting process and not applied after the extraction
of the factors as is done in eigenvector-based methods. Rotational freedom can
be reduced by having known zero values in either the G
or F matrices and forcing the solution to those values. Since
rotations really represent addition and subtractions [Paatero
and Tapper, 1994], the combination of zero values and
non-negativity constraints reduces the rotational ambiguity.
One
of the ways that rotations can be controlled in PMF2 is by using the parameter
FPEAK. By setting a non-zero value of FPEAK, the routine is forced to add one G
vector to another and subtract the corresponding F factors from each other and
thereby yield more physically realistic solutions. The method requires a
complicated mathematical process which is not described here [see Paatero, 1997]. The degree of rotational freedom is reduced
if there are real zeroed values in the true F and G matrices. Then for positive
FPEAK, zeroes in the F matrix restrict subtractions since no resulting value
can become negative. Alternatively, a negative FPEAK causes subtractions in the
G matrix and those subtractions are restricted if there zeroes in the matrix.
If there are a sufficient number of zero values both in F and in G,
then the solution is rotationally unique: there are no possible rotations.
However, this case is rare.
Experience
for real data sets has shown that positive, non-zero FPEAK values generally
yield more realistic results. There is no theoretical basis for choosing a
particular value of FPEAK. However, it is important to examine the Q value.
Since the rotation
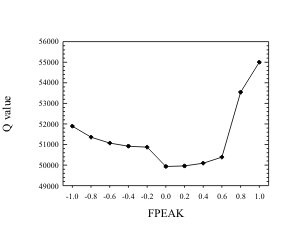
Figure 4. Plot of Q
as a function of FPEAK for a fine particle data set from
is integrated into the optimization scheme, the Q can change with the rotation. If the rotation forces the fit too away from the original Q, then the value of FPEAK should be moved toward zero. Figure 5 shows the behavior that has been observed for a number of data sets when Q is examined as a function of FPEAK. Typically the highest FPEAK value before the substantial rise in Q yielded the most physically interpretable source profiles. It has also been found in several cases that when examining the regression of the mass against the G values, FPEAK values can be varied to yield non-negative scaling factors while retaining physically reasonable source profiles.
The
imposition of external information on the solution is another way in which PMF
can control rotations. If specific values of profiles or time series are known
to be zero, then it is possible to force the solution toward zero for those
values through appropriate settings of Fkey and Gkey values. Details of setting up the input files are in the
PMF User Guide.
When
analyzing
The
analysis of
Error
Estimates for the PMF Results
It
is useful to have an estimate of the uncertainties in the elements of the F
and G that have been calculated using PMF2. It is possible to estimate
uncertainties using the process originally described by Roscoe and Hopke [1981]
and described in detail by Malinowski [1991]. The errors in the elements of one
matrix are estimated based on the errors in the ambient concentration values
and assuming that the other matrix is error-free. Each matrix (F or G)
is treated similarly in turn such that an uncertainty is associated with each
matrix element. Error models are currently under development that may produce
better estimates for the PMF analysis results.
Mass
Apportionment
The
results of the PMF analysis reproduce the data and ensure that the source
profiles and mass contributions are non-negative. However, it has not yet taken
into account the measured mass. In addition the results are uncertain relative
to a multiplicative scaling factor. Again a “1" can be introduced into
equation 1.
If we have a
sufficiently detailed chemical analysis such that those species that were not
measured can either be assumed to be strongly correlated to measured species or
represent sources that add negligible mass to the particulate matter samples, then
the sum of the source contributions, gkj
values, should be equal to the measured PM mass. Using this external
information, the scaling constants, sk,
can be determined by regressing the measured mass against the estimated source
contribution values.
This regression
provides several useful indicators of the quality of the solution. Clearly each
of the sk values
must be non-negative. If the regression produces a negative value, then it
suggests that too many factors have been used. The source profiles need to be
scaled by dividing the fik value by sk. Once
the profiles are scaled, they can be summed and it can be determined if the sum
of a source profile exceeds 100% (1000 ng/μg).
In this case, it suggests that too few factors may have been chosen. Although
it is desirable to require that the sk
values be statistically significant, there can be weak or aperiodic
sources for which these scaling coefficients may have high uncertainties.
Use of Complex
Factor Analysis Models
To
present the expanded factor analysis approach, the model is described from the
viewpoint of one source, denoted by p. In reality, there are several
sources and the observed concentrations are sums of contributions due to all
sources, p=1,..., P. In the customary
bilinear analysis, the contribution rijp
of source p on day i to concentration
of chemical species j is represented by the product gipfjp,
where gip corresponds to the
strength of source p on day i, and fjp corresponds to the concentration of
compound j in the emission signature of source p.
In
the present expanded PMF analysis, the bilinear equation (1) is augmented by
another more complicated set of equations that contain modeling information. In
its most basic form, the contribution rijp
of source p is represented by the following expression:
The known values δi and vi
indicate wind direction and wind speed on day i.
The symbols D and V represent matrices, consisting of unknown
values to be estimated during the fitting process. Their columns numbered p
correspond to source number p. Because of typographic reasons, their
indices are shown in parentheses, not as subscripts. The index value δi for day i is
typically obtained by dividing the average wind direction of day i (in degrees) by ten and rounding to nearest
integer. As an example, if source 2 comes strongly from the wind direction at
90°, then the element D(9,2) is likely to become large. The values vi are obtained from a chosen
classification of wind speeds. The following classification was used in this
work: 0 - 1.5 - 2.5 - 3.5 - 5.8 - ¥ m/s. Thus, vi=2 for such days when the average wind
speed is between 1.5 and 2.5 m/s.
In component form, the equations of the model are
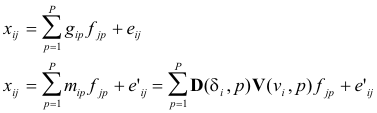
(15)
The
notation mip does not indicate a factor element to be determined, such as gip, but the expression defined by the
physical model in question. In different physical models, mip will correspond to different
expressions. Because the variability of mip is restricted by the model, the second set of equations (3) will produce a
significantly poorer fit to the data than the first set of equations (3). The
physical model, mip,
is one of multiple possible models depending on the understanding of the system
under study while the mass balance in the first set of equations should be much
more applicable. Thus, the error estimates connected with the second set of
equations must be (much) larger than the error estimates connected with the
first set of equations.
The
task of solving this expanded PMF model means that values of the unknown factor
matrices G, F, D, and V are to be determined so that the model fits the data as
well as possible. In other words, the sum-of-squares value Q, defined by
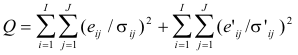(16)
is minimized with respect to the matrices G, F, D, and
V, while the residuals eij and e’ij are determined by equations (16).
The error estimates σ’ij must be specified
(much) larger than the corresponding error estimates σij.
Since
there are other sources of variation such as weekend/weekday source activity
patterns or seasonal differences in emission rates or in atmospheric chemistry,
additional factors are included in the model. In this case, wind direction,
wind speed, time of year, and weekend/weekday will be used. In this case, 24
one-hour average values are available for wind speed and direction. Time
of year will be aggregated into six two-month periods or seasons,
indicated for each day i by the index
variables σi. (The Greek letter σ is used
for two purposes: σij indicates the error
estimates of data values, while σi indicates
the season number for day i.). For the values i=1 to i=60, σi=1, meaning that January and February belong
to the first season. For the values i=61 to i=121, σi=2,
and so on.
Instead
of the basic equation (15), the non-linear dependencies are now defined by the
following multilinear expression:
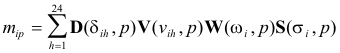(17)
where D(δih, p) is the element of D with
the index for the wind direction during hour h of day i for the pth source,
V(νih, p) is the element of V
with the index for the wind speed during hour h of day i for the pth
source, W(ωi, p) is the
element of W with the index corresponding to day i
for the weekday/weekend factor for the pth
source, and S(σi, p) is the element
of S with the index corresponding to the time-of-year classification of
day i for the pth
source. Each of these matrices, D, V, W, and S,
contain unknown values to be estimated in the analysis. The specific factor
elements used to fit a particular data point are selected based on the hourly
(D, V) or daily (W, S) values of the corresponding variables. Thus, these
auxiliary variables are not fitted, but serve as indicators to the values to be
fitted.
The
expanded model to be fitted consists thus of the basic bilinear equations plus a
set of multilinear equations specifying the physical
model:
(18)
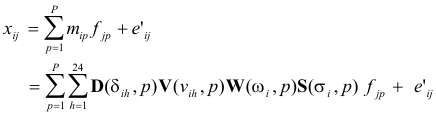
(19)
The multilinear engine (ME) was used to solve this problem with
non-negativity required for all of the elements of the matrices being estimated
[Paatero, 1999].
This
approach was first applied to simulated data previously used in an EPA workshop
on advanced factor models and showed that the expanded model permitted more
sources to be identified and accurately apportioned [Paatero
and Hopke, 2002]. The wind direction factor was quite effective in pointing at
the specific point sources contributing to the particulate matter mass.
It
has now been applied to real data sets [Kim et al., 2003c]. In this
study when compared to the standard PMF2 analysis of the same data [Kim et
al., 2003a], the expanded model provides the extraction of additional
factors. Particularly it appears to permit the separation of the contributions
of spark-ignition (gasoline) from diesel vehicle emissions. This model has also
been applied to high time resolution gaseous organic compound (VOC) data
collected in
In
addition to this expanded version of the factor analysis model, the multilinear engine has been used to explore other models
for data. Hopke et al. [2003] have analyze a
complex set of personal exposure data. The particle samples were collected with
personal samplers (PEM) from 10 elderly subjects, their apartments, a central
indoor location, and outdoors. The PEM data were analyzed using a complex model
with a target for soil that included factors that are common to all of the
types of samples (external factors) and factors that only apply to the data
from the individual and apartment samples (internal factors). From these
results, the impact of outdoor sources and indoor sources on indoor
concentrations were assessed. The identified external factors were sulfate,
soil, and an unknown factor. Internal factors were identified as gypsum or wall
board, personal care products, and a factor representing variability not
explained by the other indoor sources. The latter factor had a composition
similar to outdoor particulate matter and explained 36% of the personal
exposure. External factors contributed 63% to personal exposure with the
largest contribution from sulfate (48%).
Finally,
a special model was developed to examine the spatial variation of PM2.5
mass measurements across the eastern
SUMMARY
Over
the past decade, positive matrix factorization has evolved in terms of improved
programs and growing use in analyzing atmospheric compositional data. PMF2 is
now being widely applied to such data and has now become an accepted data
analysis tool. There remains a considerable level of experienced required to
use PMF because there remain problems of rotational ambiguity in the solutions
that has not yet been resolved. Research is continuing on this problem and is
likely to provide additional guidance in the near future.
Recent
development work has been examining new, complex models that are capable of
providing improved source attribution and resolution. These models are able to
incorporate a variety of additional information such as wind speed and
direction and thereby improve the source apportionment. They offer the
possibility of improved analyses, but will require further study before they
can become routine analysis tools.
REFERENCES
Anderson, M.J., Miller, S.L., Milford, J.B. (2001)
Source Apportionment of Exposure to Toxic Volatile Organic Compounds Using
Positive Matrix Factorization, J. Exp. Anal. Environ. Epidem. 1: 295-307
(2001).
Anttila, P., P. Paatero, U. Tapper, and O. Järvinen (1995)
Application of Positive Matrix Factorization to Source Apportionment: Results
of a Study of Bulk Deposition Chemistry in
Begum, B.A., E. Kim, S.K. Biswas,
P.K. Hopke (2004) Investigation Of Sources Of Atmospheric Aerosol At Urban And
Semi-Urban Areas In
Buzcu, B., Fraser, M.P., Kulkarni,
P., Chellam, S. (2003) Source Identification and
Apportionment of Fine Particulate Matter in Houston, Tx,
Using Positive Matrix Factorization, Environmental Engineering Science
20: 533-545.
Chueinta, W., P.K. Hopke and P. Paatero
(2000) Investigation of Sources of Atmospheric Aerosol Urban and
Suburban Residential Areas in
Chueinta, W., P.K. Hopke and P. Paatero
(2004) Multilinear Model for Spatial Pattern Analysis
of the Measurement of Haze and Visual Effects Project, Environ. Sci. Technol. 38, 544-554.
Claiborn, C.S., Larson, T., Sheppard, L.
(2002) Testing the metals hypothesis in
Currie,
Gao, S., Hegg, D.A., Jonsson, H. (2003) Aerosol Chemistry, and Light-Scattering
and Hygroscopicity Budgets During Outflow from East
Asia, J. Atmos. Chem. 46:55-88 (2003).
Hien, P.D., V.T. Bac, N.T.H. Thinh (2004) PMF receptor modelling
of fine and coarse PM10 in air masses governing monsoon conditions
in Hanoi, northern Vietnam, Atmospheric Environ. 38: 189-201.
Henry, R.C. (1987) Current Factor Analysis Models are
Ill-Posed, Atmospheric Environ. 21:1815-1820.
Henry, R.C. (1991) Multivariate Receptor Models, In: Receptor
Modeling for Air Quality Management, P.K. Hopke, ed., Elsevier Science
Publishers,
Hopke, P.K. (1985) Receptor Modeling in
Environmental Chemistry, John Wiley & Sons, Inc.,
Hopke,
P.K., ed. (1991) Receptor Modeling for Air Quality Management, Elsevier
Science,
Hopke, P.K.,P. Paatero, H. Jia, R.T. Ross, and R.A. Harshman
(1998) Three-Way (PARAFAC) Factor Analysis: Examination and Comparison of
Alternative Computational Methods as Applied to Ill-Conditioned Data, Chemom. Intel. Lab. Syst. 43:25-42.
Hopke, P.K., Z. Ramadan, P. Paatero,
G. Norris, M. Landis, R. Williams, and C.W. Lewis (2003) Receptor Modeling of
Ambient and Personal Exposure Samples: 1998 Baltimore Particulate Matter
Epidemiology-Exposure Study, Atmospheric Environ. 37: 3289-3302.
Huang, S., K.A. Rahn and R. Arimoto (1999) Testing and Optimizing Two Facot-Analysis Techniques on Aerosol at Narragansett,
Huber,
P. J. (1981) Robust Statistics, John Wiley,
Juntto, S. and P. Paatero
(1994) Analysis of daily precipitation data by positive matrix factorization, Environmetrics 5:127-144.
Kim, E. and P.K. Hopke (2004a) Source apportionment of
fine particles at
Kim, E. and P.K. Hopke (2004b)
Improving Source Identification of Fine Particles in a rural
Kim, E., Hopke, P.K., Edgerton, E. (2003a) Source
Identification of
Kim, E., Larson, T.V., Hopke, P.K., Slaughter, C.,
Sheppard, L.E., Claiborne, C. (2003b) Source Identification of PM2.5 in an Arid
Northwest U.S. City by Positive Matrix Factorization, Atmospheric Res.
66: 291–305.
Kim, E., P.K. Hopke, P. Paatero,
and E.S. Edgerton (2003c) Incorporation of Parametric Factors into Multilinear Receptor Model Studies of
Kim, E., P.K. Hopke, and E.S.
Edgerton, 2004. Improving source
identification of
Lawson, C.L. and R.J. Hanson (1974) Solving
Least-Squares Problems, Prentice-Hall,
Lee, E., C.K. Chan, and P. Paatero
(1999) Application of Positive Matrix Factorization in Source Apportionment of
Particulate Pollutants in
Lee, P.K.H., Brook, J.R., Dabek-Zlotorzynska,
E., Mabury, S.A. (2003) Identification of the Major
Sources Contributing to PM2.5 Observed in Toronto, Environ. Sci. Technol. 37: 4831-4840
(2003).
Lee, J.H., Y. Yoshida, B.J. Turpin, P.K. Hopke, and R.L.
Poirot (2002) Identification of Sources Contributing
to the Mid-Atlantic Regional Aerosol, J. Air Waste Manage. 52:1186-1205.
Malinowski,
E.R. (1991) Factor Analysis in Chemistry, Wiley,
Maykut, NN, Lewtas, J., Kim, E.,
Larson, T.V. (2003) Source Apportionment of PM2.5 at an Urban IMPROVE Site in
Miller, S.L.,
Paatero, P. (1997) Least Squares
Formulation of Robust, Non-Negative Factor Analysis, Chemom. Intell. Lab. Syst. 37:23-35.
Paatero, P. (1999)The Multilinear Engine --- a Table-driven Least Squares Program
for Solving Multilinear Problems, Including the n-way
Parallel Factor Analysis Model, J. Computational and Graphical Stat. 8: 854-888.
Paatero, P. and U. Tapper
(1993) Analysis of Different Modes of Factor Analysis as Least Squares Fit
Problems, Chemom. Intell. Lab. Syst. 18:183-194.
Paatero, P. and U. Tapper (1994)
Positive matrix factorization: a non-negative factor model with optimal
utilization of error estimates of data values, Environmetrics
5:111-126.
Paatero, P. and P.K. Hopke (2002) Utilizing Wind Direction
and Wind Speed as Independent Variables in Multilinear
Receptor Modeling Studies, Chemom. Intell.
Lab. Syst. 60: 25-41.
Paatero, P. and P.K. Hopke, 2003. Discarding or Downweighing
High-Noise Variables in Factor Analysis Models, Anal. Chim. Acta 490: 277-289.
Paatero, P., P.K. Hopke, X.H. Song, Z. Ramadan (2002)
Understanding and Controlling Rotations in Factor Analytic Models, Chemom. Intell. Lab. Syst. 60: 253-264.
Paatero, P., P.K. Hopke, J. Hoppenstock,
and S. Eberly, (2003) Advanced Factor Analysis of
Spatial Distributions of PM2.5 in the
Paterson, K.G. , J.L. Sagady, D.L. Hooper , S.B. Bertman
, M.A. Carroll , and P.B. Shepson (1999) Analysis of
Air Quality Data Using Positive Matrix Factorization, Environ. Sci. Technol. 33: 635-641
Polissar, A.V., P.K. Hopke, W.C. Malm,
J.F. Sisler (1996) The Ratio of Aerosol Optical
Absorption Coefficients to Sulfur Concentrations, as an Indicator of Smoke from
Forest Fires when Sampling in Polar Regions, Atmospheric Environ. 30:1147-1157.
Polissar, A.V., P.K. Hopke, W.C. Malm,
J.F. Sisler (1998) Atmospheric Aerosol over
Polissar, A.V., P.K. Hopke, P. Paatero,
Y. J. Kaufman, D. K. Hall, B. A. Bodhaine, E. G.
Dutton and J. M. Harris (1999) The Aerosol at Barrow, Alaska: Long-Term Trends
and Source Locations, Atmospheric Environ. 33: 2441-2458.
Polissar, A.V. , P.K. Hopke, and R.L.
Poirot (2001b) Atmospheric Aerosol over
Prendes, P., Andrade, J.M., Lopez-Mahia,
P., Prada, D. (1999) Source Apportionment of
Inorganic Ions in Airborne Urban Particles from
Qin, Y., Oduyemi, K., (2003)
Atmospheric Aerosol Source Identification and Estimates of Source Contributions
to Air Pollution in
Qin, Y., Oduyemi,
K., Chan, L.Y. (2002) Comparative Testing of PMF and CFA Models, Chemom. Intell. Lab. Syst. 61: 75-87 (2002).
Ramadan, Z., X.-H. Song, and P.K. Hopke (2000) Identification of Sources
of
Roscoe, B.A. and P.K. Hopke (1981) Error Estimation
of Factor Loadings and Scores Obtained with Target Transformation Factor
Analysis, Anal. Chim. Acta 132:89-97.
Wang, D. and P. Hopke (1989) The Use of Constrained
Least-Squares to Solve the Chemical Mass Balance Problem, Atmospheric
Environ. 23:2143-2150.
Xie, Y.-L., P. K. Hopke, P. Paatero, L. A. Barrie and S.-M. Li (1999a) Identification of Source Nature and
Seasonal Variations of Arctic Aerosol by the Multilinear
Engine, Atmospheric Environ. 33: 2549-2562.
Xie, Y. L., Hopke, P., Paatero, P., Barrie, L. A., and Li, S. M. (1999b). Identification of source nature and
seasonal variations of Arctic aerosol by positive matrix factorization. J.
Atmos. Sci. 56:249-260.
Yakovleva, E., P.K. Hopke and L. Wallace (1999) Receptor
Modeling Assessment of PTEAM Data, Environ. Sci. Technol. 33: 3645-3652.
Zhao, W., P.K. Hopke, and T. Karl (2004) Source
Identification of Volatile Organic Compounds in